Зависимость между синусом, косинусом и тангенсом одного и того же угла. Открытый урок по алгебре на тему "Зависимость между синусом и косинусом одного и того же угла" (10 класс)

⁰

А синуса график волна за волной
По оси абсцисс убегает.

Из студенческой песни.

ЦЕЛИ И ЗАДАЧИ УРОКА:

ОБРАЗОВАТЕЛЬНАЯ: вывод формул зависимости между синусом, косинусом и тангенсом одного и того же угла (числа); обучение применению этих формул для вычисления значений синуса, косинуса, тангенса числа по заданному значению одного из них.
РАЗВИВАЮЩАЯ: учить анализировать, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия..
ВОСПИТАТЕЛЬНАЯ: воспитание добросовестного отношения к труду и положительного отношения к знаниям.

ЗДОРОВЬЕ СБЕРЕГАЮЩАЯ: создание комфортного психологического климата на уроке, атмосферы сотрудничества: ученик – учитель.

МЕТОДИЧЕСКОЕ ОСНАЩЕНИЕ УРОКА:

МАТЕРИАЛЬНО-ТЕХНИЧЕСКАЯ БАЗА: кабинет математики.

ДИДАКТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УРОКА: учебник, тетрадь, плакаты по теме урока, таблицы, компьютер, диски, экран, проектор.

МЕТОДЫ ДЕЯТЕЛЬНОСТИ: групповая и индивидуальная работа за партой и у доски.

ТИП УРОКА: урок усвоения новых знаний.

ХОД УРОКА

1. Организационный момент: приветствие, проверка явки учащихся, заполнение журнала.

2. Проверка готовности учащихся к уроку: настрой учащихся на работу, доведение до них плана урока.

3. Анализ ошибок домашнего задания. На экране - картинка с верно выполненным домашним заданием. Каждый ученик проверяет с подробным фронтальным объяснением и отмечает правильность выполнения в рабочей карте урока.

РАБОЧАЯ КАРТА УРОКА.

С/о – самооценка.

О/т – оценка товарища.

4. Актуализация знаний, подготовка к восприятию нового материала.

Следующий этап нашего урока-диктант. Записываем кратко ответы – чертеж у нас на слайде.

Диктант (устное повторение необходимых сведений):

1. Дайте определение:

синуса острого угла А прямоугольного треугольника;
косинуса острого угла В прямоугольного треугольника;
тангенса острого угла А прямоугольного треугольника;
котангенса острого угла В прямоугольного треугольника;
какие ограничения накладываем мы на синус и косинус при определении тангенса и котангенса острого угла прямоугольного треугольника.

2. Дайте определение:

синуса угла a a .
косинуса угла a через координату (какую) точки, полученной поворотом точки (1;0) вокруг начала координат на угол a .
тангенса угла a .
котангенса угла a .

3. Записать знаки синуса, косинуса, тангенса, котангенса для углов, полученных поворотом точки Р(1;0) на угол

4. Для всех этих углов указать четверти координатной плоскости.

Ребята проверяют диктант по слайду вместе с учителем, объясняя каждое высказывание и выставляя себе оценку в рабочую карту урока.

5. Из истории тригонометрии. Современный вид тригонометрии придал крупнейший математик 18 столетия Леонард Эйлер – швейцарец по происхождению, долгие годы работавший в России и являвшийся членом Петербургской академии наук. Он ввел известные определения тригонометрических функций, сформулировал и доказал формулы приведения, с которыми вам еще предстоит встретиться, выделил классы четных и нечетных функций.

6. Введение нового материала:

Главное не просто сообщить учащимся конечные выводы, а сделать учащихся как бы участниками научного поиска: поставив вопрос, так, чтобы они, разбудив свою любознательность, включились в исследование, что способствует достижению более высокого уровня умственного развития учащихся.

Поэтому при введении нового материала я создаю проблемную ситуацию – как легче и рациональней установить зависимость между синусом и косинусом одного и того же угла – через уравнение единичной окружности или через теорему Пифагора.

Класс разбивается по вариантам на первый и второй вариант – на экране слайд с условием и чертежами, решения пока нет.

1 вариант устанавливает зависимость между синусом и косинусом через уравнение окружности с центром в начале координат и радиусом, равным 1x 2 +y 2 =1; sin 2 +cos 2 =1.

2 вариант устанавливает зависимость между синусом и косинусом через теорему Пифагора – в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: OB 2 +AB 2 =OA 2 - и получаем sin 2 +cos 2 =1.

Сравнивают результаты, делают выводы: главный – равенство выполняется при любых значениях входящих в него букв? Ученики должны ответить, что это тождество

(на слайде показывается верное решение, как для первого, так и для второго вариантов).

Мы получили равенство справедливое при любых значениях входящих в него букв. Как называются такие равенства? Правильно – тождества.

Вспомним – какие еще тождества мы с вами знаем в алгебре – формулы сокращенного умножения:

a 2 -b 2 =(a-b)(a+b),

(a-b) 2 =a 2 -2ab+b 2 ,

(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 2 ,

(a-b) 3 =a 3 -3a 2 b+3ab 3 -b 3 ,

a 3 -b 3 =(a-b)(a 2 +ab+b 2),

a 3 +b 3 =(a+b)(a 2 -ab+b 2).

Следующая проблема – а для чего мы вывели основное тригонометрическое тождество – sin 2 +cos 2 =1.

Правильно – для нахождения по одному известному нам значению синуса, косинуса или тангенса – значений всех остальных функций.

Вот теперь мы с вами всегда сможем пользоваться основным тригонометрическим тождеством, но главное – для одного и того же аргумента.

Применение полученных знаний:

1 ВАРИАНТ – выразить синус через косинус угла.

2 вариант – выразить косинус через синус угла. На слайде верный ответ

Вопрос учителя – никто не забыл проставить знаки +и - ? Каким может быть угол? – любым.

В этих формулах знак перед корнем зависит от чего? от того, в какой четверти расположен угол (аргумент) тригонометрической функции, которую мы определяем.

Выполняем у доски 2 ученика №457. – 1 – й вариант - 1, 2-й вариант - 2.

На слайде – верное решение.

Самостоятельная работа на узнавание основного тригонометрического тождества

1. найти значение выражения:

2. выразить число 1 через угол a , если

Идет взаимопроверка – по готовому слайду и оценивание работ – как самооценкой, так и оценкой товарища.

6. Закрепление нового материала (по технологии Г.Е.Хазанкина – технология опорных задач).

ЗАДАЧА 1. Вычислить ……….., если ………………………………………………………………….

1 ученик у доски самостоятельно – затем слайд с правильным решением.

ЗАДАЧА 2. Вычислить……………., если………………………………………………………………..

2-й ученик у доски, затем слайд с верным решением.

7. Физкультминутка.Я знаю, что вы уже взрослые и считаете, что совсем не устали, особенно сейчас, когда урок идет так активно, что время для нас как –бы и удлиняется– по теории относительности А.Эйнштейна, но давайте проведем гимнастику для сосудов головного мозга:

повороты и наклоны головы вправо – влево, вверх – вниз
массаж плечевого пояса и кожи головы – руки от кисти, лицо и затылок – сверху вниз.
плечи поднять вверх и расслабленно “сбросить” вниз. Каждое упражнение выполняем 5-6 раз!

Выясним теперь зависимость между тангенсом и котангенсом………………………………………………………………………………………………………

Идет новое исследование на тему – каким может быть угол во втором тригонометрическом тождестве?

ГЛАВНОЕ – ВЫЯСНЕНИЕ МНОЖЕСТВА, НА КОТОРОМ ЭТИ РАВЕНСТВА ВЫПОЛНЯЮТСЯ. ОТМЕТИТЬ НА РИСУНКЕ ТОЧКИ, В КОТОРЫХ ТАНГЕНС И КОТЕНГЕНС УГЛА НЕ СУЩЕСТВУЕТ.

3-й ученик у доски. Равенства справедливы при……………………….

ЗАДАЧА3. Вычислить………, если………………………….

ЗАДАЧА 4. Вычислить…………….. если ………………………………………………………………

Остальные учащиеся работают у себя в тетрадях.

1 ОПОРА………………………………………………………………………………………………

2 ОПОРА………………………………………………………………………………………………

3 ОПОРА. Применение основного тригонометрического тождества к решению задач.

8. Кроссворд. Анатоль Франс сказал как-то: “Учиться надо весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.

Для проверки знаний по данной теме вам предлагается кроссворд.

Раздел математики, изучающий свойства синуса, косинуса, тангенса…
Абсцисса точки на единичной окружности.
Отношение косинуса к синусу.
Синус – это…..точки на единичной окружности.
Равенство не требующее доказательства и верное при любых значениях входящих в него букв. Называется……

Проверив кроссворд, ребята выставляют себе оценки в рабочую карту урока. Учитель выставляет оценки тем ученикам, которые особенно активно проявили себя на уроке. Итог – средний балл за работу на уроке.

9. Инструктаж учителя по выполнению домашнего задания.

10. Подведение учителем итогов урока.

11. Домашнее задание: параграф 25 (до задачи 5), №459 (четные), 460 (четные), 463*(4). Учебник Ш.А Алимов “Алгебра и начала анализа”., 10-11, “Просвещение”., М., 2005г.

Тема: Тригонометрические формулы (25 часов)
Урок 6 – 7: Зависимость между синусом, косинусом и тангенсом одного и того же угла.
Цель: изучить зависимость между синусом, косинусом и тангенсом одного и того же угла. Для достижения поставленной цели необходимо:

Знать:

формулировки определений основных тригонометрических функций (синуса, косинуса и тангенса); знаки тригонометрических функций по четвертям; множество значений тригонометрических функций; основные формулы тригонометрии.

Понимать:

что пользоваться основным тригонометрическим тождеством можно только для одного и того же аргумента; алгоритм вычисления одной тригонометрической функции через другую.

Применить:

нужную формулу

Анализ:

анализировать ошибки в логике рассуждения.

Синтез:

предложить свой способ решения примеров; составить кроссворд, используя полученные знания.

Оценка:

знаний и умений по данной теме для использования в других разделах алгебры.

Оборудование: макет тригонометрической окружности, раздаточный справочный материал с формулами и таблицами значений тригонометрических функций, компьютер, мультимедийный проектор, презентация, листы с заданиями для самостоятельной работы.Ход урока:

Организационный момент.

Приветствие. Сообщение цели урока и плана работы на уроке.

Актуализация знаний и умений.

Учащимся раздаются карты урока и даются пояснения как с ними работать. На экран выводятся вопросы; учащиеся записывают ответы в тетрадь; преподаватель выводит на экран правильный ответ. После окончания опроса учащиеся выставляют баллы в карту урока для Задания № 1.

В какой четверти находится угол в 1 радиан и чему он примерно равен? (В I четверти, 1 рад. 57,3 0).

Какое слово пропущено в определение функции синус? Синусом угла  называется............ точки единичной окружности. (Ордината)

Какое слово пропущено в определении функции косинус? Косинусом угла  называется............ точки единичной окружности (Абсцисса).

Какие значения может принимать синус?

()

Объяснение нового материала.

зобразим единичную окружность с центром в точке О. Пусть при повороте радиуса ОА, равного R, на угол  получен радиус ОВ (рис. 5). Тогда по определению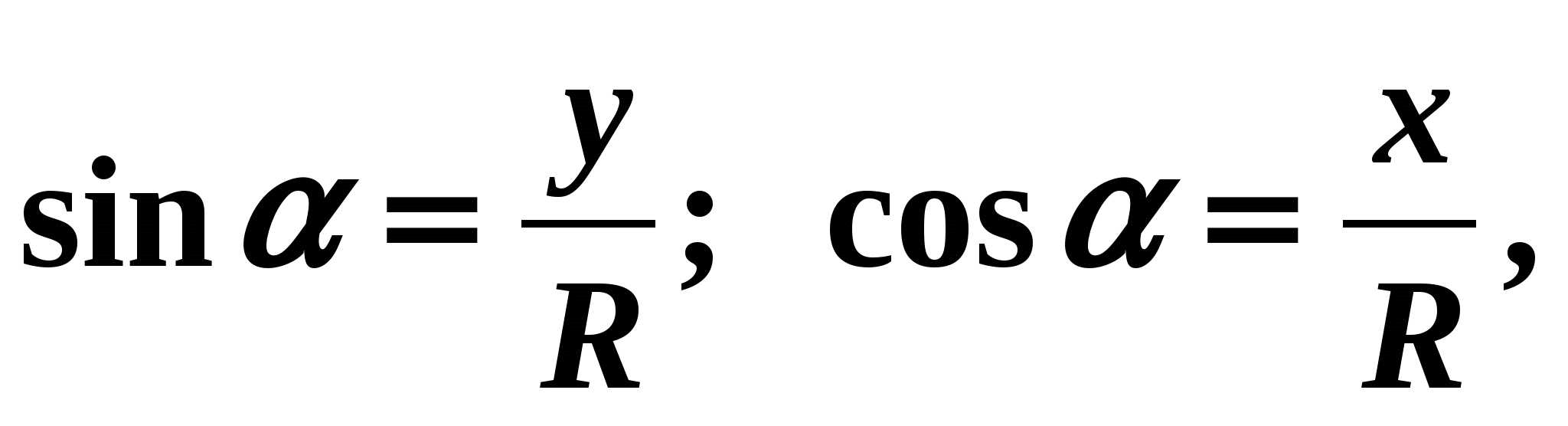

где

– абсцисса точки В,

– ее ордината. Отсюда следует, что Точка В принадлежит окружности. Поэтому ее координаты удовлетворяют уравнению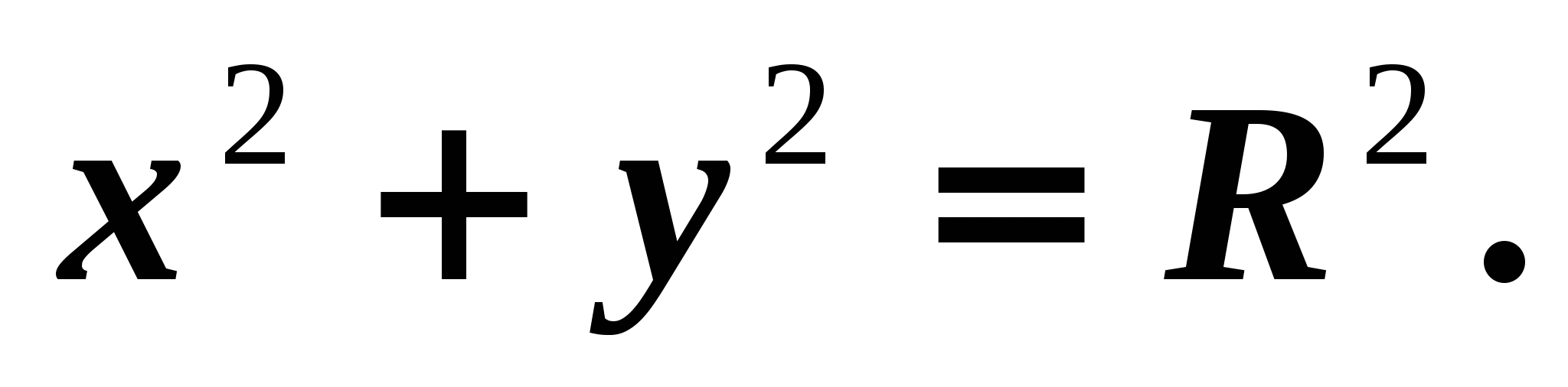

Воспользовавшись тем, что получим

(1). Мы получили равенство справедливое при любых значениях входящих в него букв. Как называются такие равенства? Правильно – тождества. Равенство (1) называется основным тригонометрическим тождеством. В равенстве (1)  может принимать любые значения. Самостоятельно завершите запись:
1.
Проверьте правильность вашей записи. Выставите себе баллы в карту урока для Задания № 2. Продолжаем. Мы вывели основное тригонометрическое тождество, а для чего оно нам нужно? Правильно – для нахождения по одному известному нам значению синуса значение косинуса и наоборот. Вот теперь мы с вами всегда сможем пользоваться основным тригонометрическим тождеством, но главное – для одного и того же аргумента. Учащимся в тетради предлагается самостоятельно выразить из основного тригонометрического тождества синус через косинус и косинус через синус. Для проверки к доске вызываются два ученика. Одному предлагается выразить синус через косинус, второму – косинус через синус. На экран выводится верный ответ:

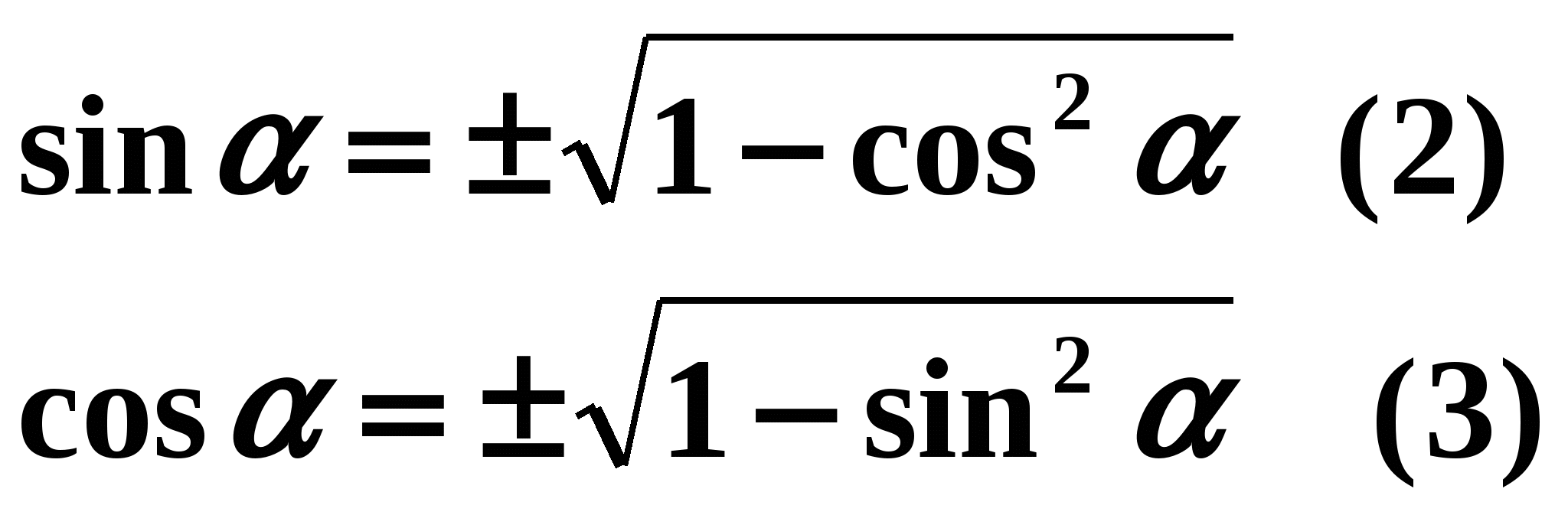Учащиеся проверяют свои ответы и выставляют баллы в карту урока для Задания № 3. В этих формулах от чего зависит знак перед корнем? (От того, в какой четверти расположен угол тригонометрической функции, которую мы определяем).
Пример 1 . Вычислить

если

Определим четверть, в которой находится угол

. Четверть – III. Вспомним, что синус в третьей четверти отрицательный, т. е. в формуле (2) перед корнем нужно поставить знак « – »: Пример 2. Вычислить

если

Определяем четверть, в которой находится угол  . Четверть – IV, косинус в четвертой четверти положителен. Поэтому в формуле (3) перед корнем нужен знак « + »:
Выясним теперь зависимость между тангенсом и котангенсом . По определению тангенса и котангенса

Перемножая эти равенства, получаем:

Из равенства (4) можно выразить

через

и наоборот:

Равенства (4) – (6) верны при всех значениях, при которых

имеют смысл, т. е. при

Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также котангенсом и синусом одного и того же аргумента. Разделив обе части равенства (1) на

, получим:

т.е.

Если обе части равенства (1) разделить на

, то будем иметь:

т.е.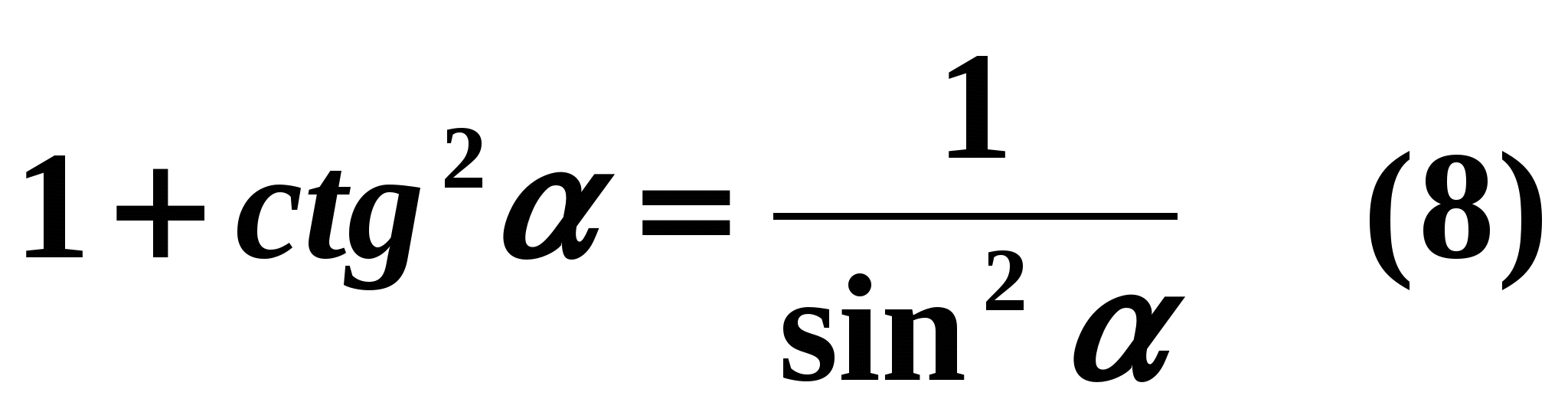

Рассмотрим примеры использования выведенных формул для нахождения значений тригонометрических функций по известному значению одной из них.
Пример 1. Найдем если известно, что

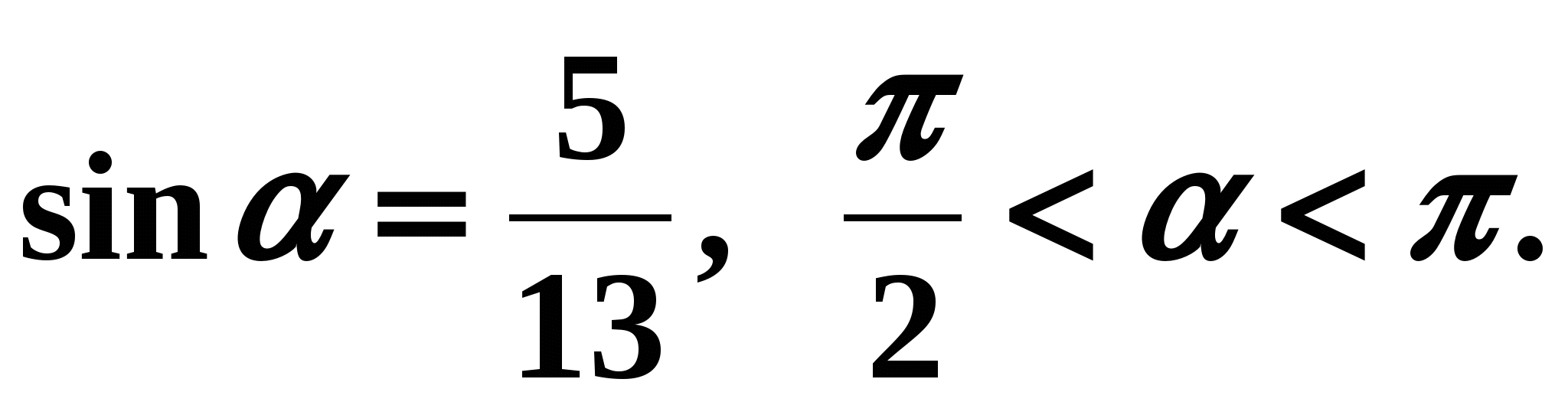Решение:

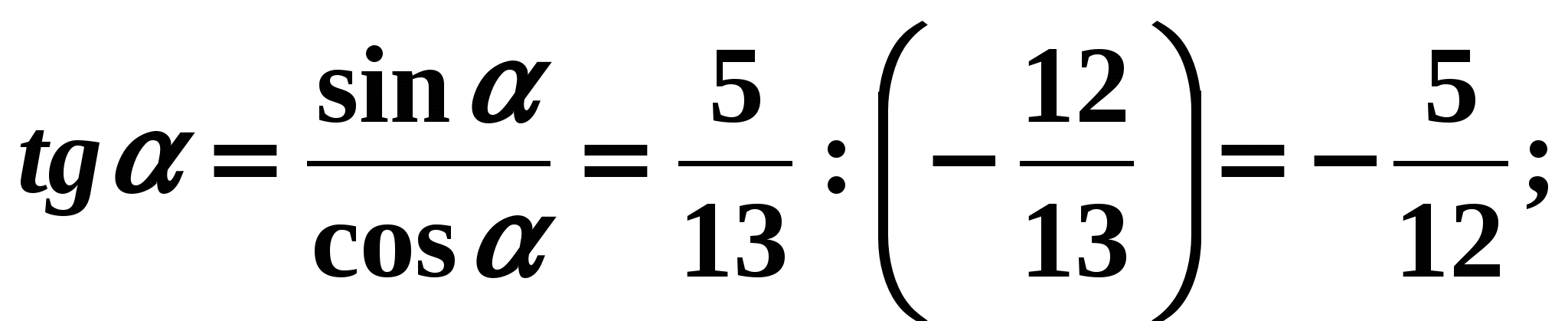
Для отыскания котангенса угла  удобно воспользоваться формулой (6):

Ответ:
Пример2. Известно, что

. Найдем все остальные тригонометрические функции. Решение:

(7).

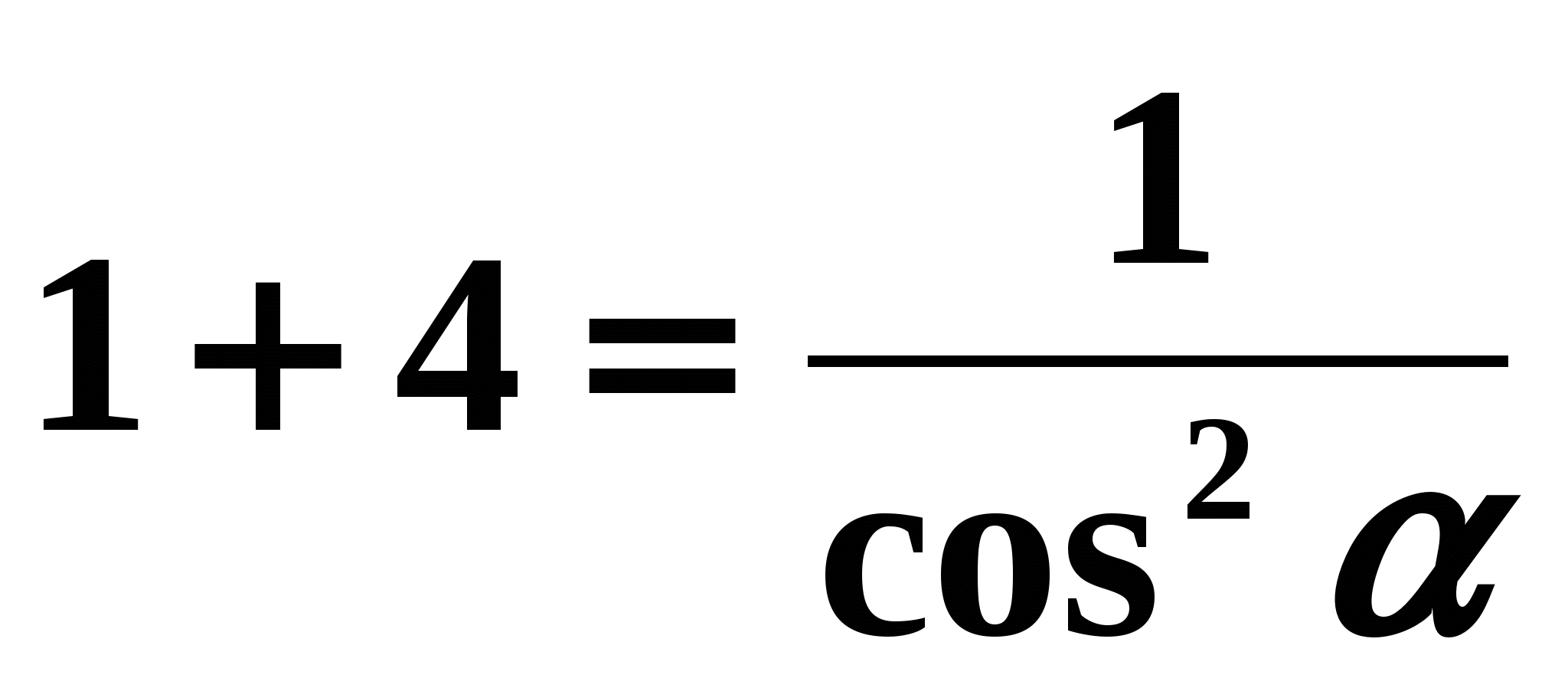. По условию задачи угол  является углом 1 четверти, поэтому его косинус положителен. Значит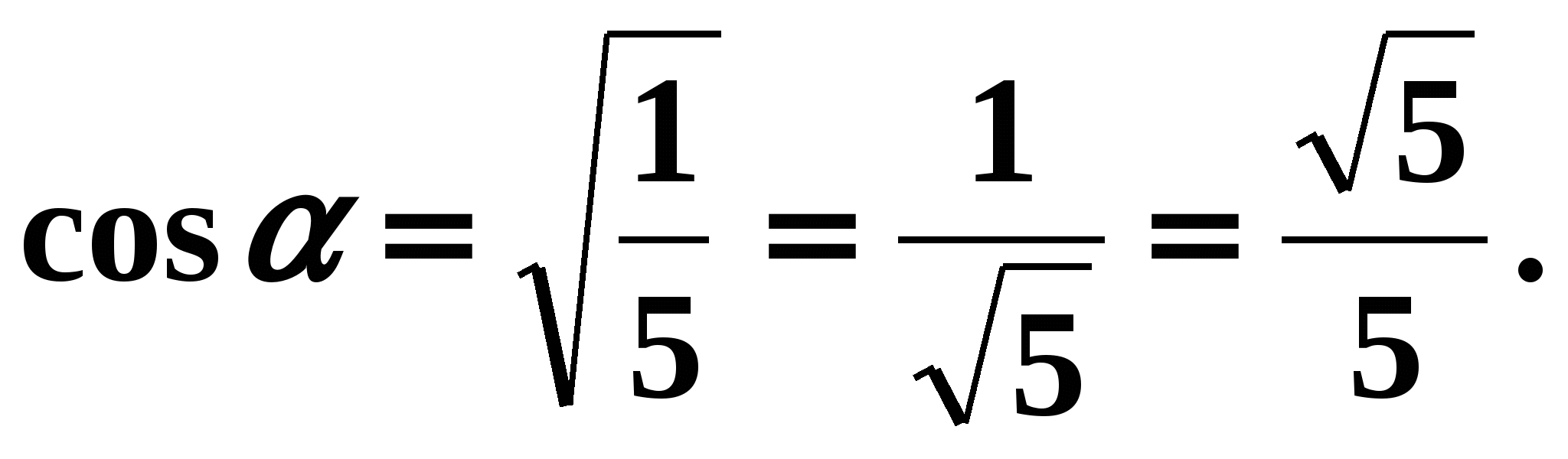

Ответ:

Установленные соотношения между тригонометрическими функциями одного и того же аргумента позволяют упрощать тригонометрические выражения.
Пример 3. Упростим выражение:

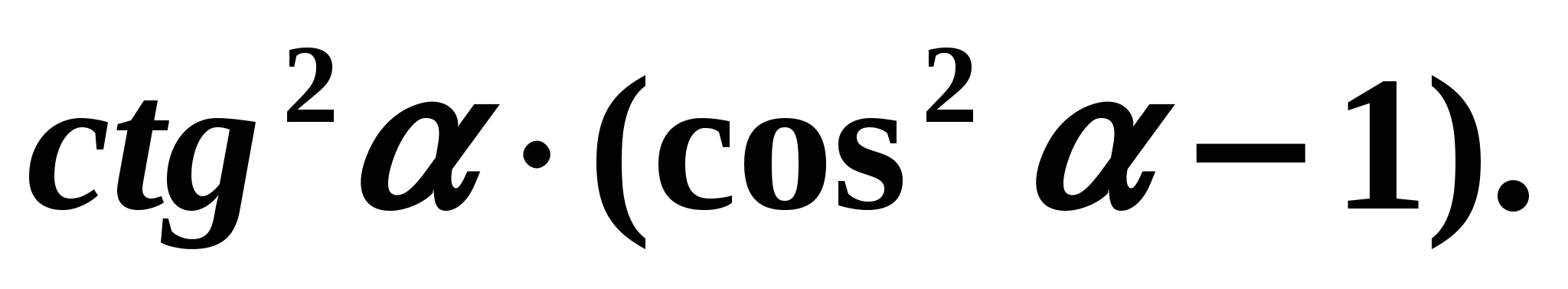Решение: Воспользуемся формулами:

. Получим:

Закрепление.

А сейчас на экране представлены рубрики самооценки по данной теме. Отметьте, на какой уровень вы бы хотели сегодня выйти.

Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, но с помощью наводящих вопросов (карточка – инструкция).

Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, используя указания преподавателя.

Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, без наводящих вопросов и указаний.

Я понял тему и могу решать примеры по алгоритму, не заглядывая в тетрадь.

Какой бы уровень вы не выбрали, сначала внимательно просмотрите все задания, которые я вам раздала, а затем выполните задание, соответствующее выбранному вами уровню (перед вами лежат задания четырех вариантов, номер варианта соответствует уровням самооценки.)

1 вариант

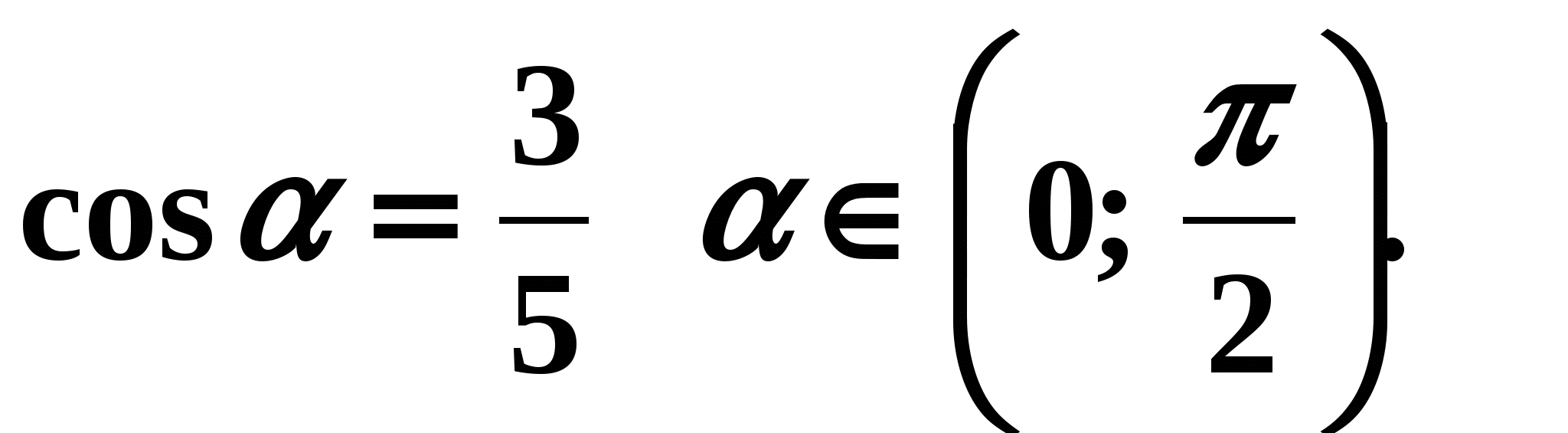Инструкция:

4 вариант

А теперь, ребята, давайте проверим ответы. На экран выводятся правильные ответы, и учащиеся проверяют свои работы и выставляют баллы в карту урока для Задания № 4. По карте урока оцените себя. Подсчитайте свои баллы и выставите их в карту.

Домашнее задание.

Записать все выведенные формулы в справочник. По учебнику №459 (3, 5), №460 (1)

Открытый урок по алгебре и началам анализа по теме: «Зависимость между синусом и косинусом одного и того же угла» (10 класс)

Цель: восприятие учащимися и первичное осознание нового учебного материала, осмысливание связей и отношений в объектах изучения

Образовательная : вывод формул зависимости между синусом и косинусом одного и того же угла (числа); обучение применению этих формул для вычисления значений синуса, косинуса по заданному значению одного из них.

Развивающая : учить анализировать, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия, развивать и совершенствовать умения применять имеющиеся у учащихся знания в различных ситуациях; развивать грамотную математическую речь учащихся, умение давать лаконичные формулировки

Воспитательная: воспитание добросовестного отношения к труду и положительного отношения к знаниям, воспитывать у учащихся аккуратность, умение слушать, высказывать свое мнение; культуру поведения.

Здоровье-сберегающая : создание комфортного психологического климата на уроке, атмосферы сотрудничества: ученик – учитель.

Знания и умения: определений основных тригонометрических функций (синуса, косинуса); знаков тригонометрических функций по четвертям; множества значений тригонометрических функций; основных формул тригонометрии. У мение правильно выбрать нужную формулу для решения конкретного задания; работать с простыми дробями; выполнять преобразование тригонометрических выражений.

Ход урока

Организационный момент:

Проверить готовность учащихся к уроку. Открытие на компьютерах сайта учителя(Приложение 1).

Устная работа по пройденной теме : «Знаки синуса, косинуса и тангенса»

На доске:

Задание:

Расставить номера четвертей координатной плоскости и определить знаки синуса, косинуса, тангенса и котангенса.

Самостоятельная работа по теме: «Знаки синуса, косинуса и тангенса»

Учащиеся открывают на сайте раздел «Задания к уроку по тригонометрии». Самопроверка

(Учащиеся выполняют задание №1, проверяют свои работы и оцениваю себя)

Объяснение нового материала

На доске:

х = … α , … ≤ cos α≤ … 2)* tg α = , α≠ …

y = … α, … ≤ sin α≤ … ctg α = , α≠ …

Задание: дописать формулы

Учитель : «Мы с вами изучили каждое понятие отдельно. Как вы считаете какую тему далее логично изучить?»

( Предполагаемый ответ: «Зависимость между этими понятиями»)

Формулируется тема урока: «Зависимость между синусом и косинусом одного и того же угла»

Учитель : «Есть несколько путей решения этой проблемы»

Используя уравнение единичной окружности

Используя теорему Пифагора

Учитель : «Давайте рассмотрим оба и выберем наиболее рациональный»

На доске:

Учащиеся выводят равенство cos 2 α + sin 2 α = 1

Учитель : «Мы получили равенство справедливое при любых значениях, входящих в него букв. Как называют такие равенства?»

( Предполагаемый ответ : тождества)

Учитель : «Вспомните, как называется тождество cos 2 α + sin 2 α = 1 »

Закрепление изученного материала

А) Учитель: «Откройте учебник стр.147, № 457(2;4)»(вызванные учащиеся решают у доски)

Б) Учитель: «Приступите к выполнению задания №2. Работаем по вариантам» (Обсуждение полученных результатов)

На доске:

1 вариант 2 вариант

Учитель: «В данных формулах перед корнем стоят знаки « ±» . От чего зависит какой знак ставить в формуле?»

(Предполагаемый ответ: «От того, в какой четверти расположен угол поворота точки P(1;0)»)

В) Учитель: «Приступите к выполнению задания №3». (Учащиеся решают задания, проверка на доске)

Подведение итогов урока

Учитель: «Молодцы! Итог урока мы подведем с помощью кроссворда» (Задание 4) (Учащиеся работают в парах за компьютером)

7) Рефлексия в форме анкетирования (приложение 2)

Учитель: «Сделайте вывод о своей работе на уроке, заполнив тест».

8) Домашнее задание

§25, №456, 457(1;3),460(1;3).

Доклад

Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.

tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}

tg \alpha \cdot ctg \alpha = 1

Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.

При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.

Нахождение тангенса и котангенса через синус и косинус

tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace

Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha} , а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha} — будет являться котангенсом.

Добавим, что только для таких углов \alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg \alpha=\frac{\cos \alpha}{\sin \alpha} .

Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha} является справедливой для углов \alpha , которые отличны от \frac{\pi}{2}+\pi z , а ctg \alpha=\frac{\cos \alpha}{\sin \alpha} — для угла \alpha , отличного от \pi z , z — является целым числом.

Зависимость между тангенсом и котангенсом

tg \alpha \cdot ctg \alpha=1

Данное тождество справедливо только для таких углов \alpha , которые отличны от \frac{\pi}{2} z . Иначе или котангенс или тангенс не будут определены.

Опираясь на вышеизложенные пункты, получаем, что tg \alpha = \frac{y}{x} , а ctg \alpha=\frac{x}{y} . Отсюда следует, что tg \alpha \cdot ctg \alpha = \frac{y}{x} \cdot \frac{x}{y}=1 . Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.

Зависимости между тангенсом и косинусом, котангенсом и синусом

tg^{2} \alpha + 1=\frac{1}{\cos^{2} \alpha} — сумма квадрата тангенса угла \alpha и 1 , равна обратному квадрату косинуса этого угла. Данное тождество справедливо для всех \alpha , отличных от \frac{\pi}{2}+ \pi z .

1+ctg^{2} \alpha=\frac{1}{\sin^{2}\alpha} — сумма 1 и квадрат котангенса угла \alpha , равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого \alpha , отличного от \pi z .

Примеры с решениями задач на использование тригонометрических тождеств

Пример 1

Найдите \sin \alpha и tg \alpha , если \cos \alpha=-\frac12 и \frac{\pi}{2} < \alpha < \pi ;

Показать решение

Решение

Функции \sin \alpha и \cos \alpha связывает формула \sin^{2}\alpha + \cos^{2} \alpha = 1 . Подставив в эту формулу \cos \alpha = -\frac12 , получим:

\sin^{2}\alpha + \left (-\frac12 \right)^2 = 1

Это уравнение имеет 2 решения:

\sin \alpha = \pm \sqrt{1-\frac14} = \pm \frac{\sqrt 3}{2}

По условию \frac{\pi}{2} < \alpha < \pi . Во второй четверти синус положителен, поэтому \sin \alpha = \frac{\sqrt 3}{2} .

Для того, чтобы найти tg \alpha , воспользуемся формулой tg \alpha = \frac{\sin \alpha}{\cos \alpha}

tg \alpha = \frac{\sqrt 3}{2} : \frac12 = \sqrt 3

Пример 2

Найдите \cos \alpha и ctg \alpha , если и \frac{\pi}{2} < \alpha < \pi .

Показать решение

Решение

Подставив в формулу \sin^{2}\alpha + \cos^{2} \alpha = 1 данное по условию число \sin \alpha=\frac{\sqrt3}{2} , получаем \left (\frac{\sqrt3}{2}\right)^{2} + \cos^{2} \alpha = 1 . Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14 .

По условию \frac{\pi}{2} < \alpha < \pi . Во второй четверти косинус отрицателен, поэтому \cos \alpha = -\sqrt\frac14=-\frac12 .

Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha} . Соответствующие величины нам известны.

ctg \alpha = -\frac12: \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3} .